
Ġ.05 0.10 0.15 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30Ĭontinuing the candy example, let us determine the probability that there is no more than 2 pieces of sour apple candy in the bag. How do you do Poisson CDF on a calculator How do you find CDF on a graphing calculator Step 1: Press the 2nd key and then press VARS then 2 to get. cdf() method of the scipy.poisson generator. In order to calculate the Poisson CDF using Python, we will use the. Note that it is skewed positive (right), that its sample space is non-negative, and that there is no upper bound to its sample space. Poisson CDF (cumulative distribution function) in Python. We know X follows a Poisson distribution because it is the number of successes measured over time (or space).įor those who like pictures, here is a graphic of the probability mass function of X. Let X be the number of defective pieces of candy manufactured in a specified week.įrom the description, we can tell that X follows a Poisson distribution with rate parameter λ = 10. These defective pieces will not kill a person, but they will cause the person’s left index finger to turn scarlet. Every week, an average of 10 pieces are defective. Unfortunately, they are not too good at it. An example of where such a distribution may arise is the following: For this problem, let X have rate parameter λ = 10. Every week, an average of 11.33 pieces are defective. P o i s s o n ( k 0) e x p ( n p) You can show that the Poisson distribution is always greater than the Binomial at k0. In fact, you can disprove this algebraically too, at k0: B i n o m i a l ( k 0) ( 1 p) n. An example of where such a distribution may arise is the following: Statistics, Inc., makes candy. This calculator will compute the cumulative distribution function (CDF) for the Poisson distribution, given the number of event occurrences and the expected number of event occurrences. The Poisson CDF > Binomial CDF at low k, so your proof is impossible.

For this problem, let X have rate parameter 11.33.
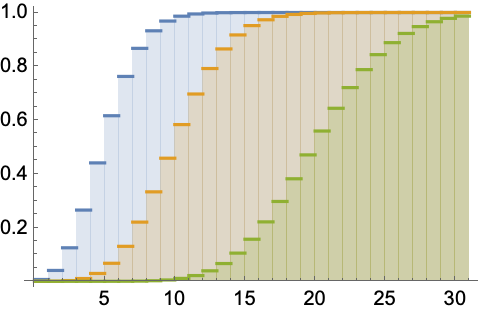

The integrand in the above integral is the density function of a gamma distribution (with the shape parameter being a positive integer). All Poisson distributions have just one parameter: average rate, λ (lambda). All Poisson distributions have just one parameter: average rate, (lambda). The relation (7) shows that the gamma survival function is the cumulative distribution function (CDF) of the corresponding Poisson distribution.
#Poisson cdf plus#
Please see the TI-84 Plus C Silver Edition guidebook for additional information.Let X be a random variable following a Poisson distribution. The syntax is as follows:įor example, given Ã=6 and x=10 find the probability for the discrete Poisson distribution: Please note that à must be any real number that is greater than zero x may be any real number or a list of real numbers. CDF of interval-arrival times in a Poisson process (Image by Author) Recollect that CDF of X returns the probability that the interval of time between consecutive arrivals will be less than or equal to some value t. The command poissoncdf( computes a cumulative probability at x for the discrete Poisson distribution with a specified mean Ã.
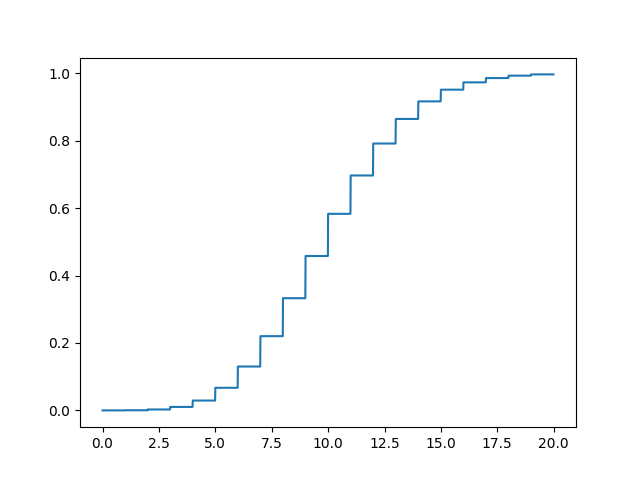
The cumulative distribution function (cdf) evaluated at k, is the probability that the random variable (X) will take a value less than or equal to k. Poisson Random Variables Examples Unfortunately there is no way to compute the CDF or ranges except by simply adding together all the individual values. How do I use the poissonpdf( ) or possioncdf( ) command on a TI-84 Plus C Silver Edition? An poisson distribution has mean and variance.
#Poisson cdf pdf#
Solution 34600: Computing a Poisson PDF and Poisson CDF on TI-84 Plus C Silver Edition.


 0 kommentar(er)
0 kommentar(er)
